مسائل على دروس رياضيات الصف الرابع الفترة الأولى من الفصل الثالث.
س ١ / اختر الإجابة الصحيحة :
- سعة حوض السمك هي :
( أ) ٤٠ كيلوجرام ، ( ب) ٤٠ لتر ، ( ج) ٤٠ جرام ، ( د) ٤٠ مللتر
شرح الإجابة : لقياس السعة نستعمل وحدتين : اللتر لقياس الأشياء التي سعتها الكبيرة و المللتر لقياس الأشياء التي سعتها صغيرة وحوض السمك سعته كبيرة
فالإجابة هي فقرة ( ب ) ٤٠ لتر.
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
- ما طول الفترة الزمنية من الساعة ٤:٢٠ مساءً إلى الساعة ٨:٠٠ مساءً ؟
( أ) ثلاث ساعات و ٤٠ دقيقة ، ( ب) ثلاث ساعات فقط ، ( ج) ثلاث ساعات و ٣٠ دقيقة
الإجابة : أحسب الزمن المُنقضي كما يلي :
٤:٢٠ ← + ساعة ← ٥:٢٠ ← + ساعة ← ٦:٢٠ ← + ساعة ← ٧:٢٠ ← + ٤٠ دقيقة ← ٨:٠٠
لحساب الدقائق ٦٠ - ٢٠ = ٤٠ دقيقة.
ساعة + ساعة + ساعة + ٤٠ دقيقة = ثلاث ساعات و ٤٠ دقيقة.
طريقة أخرى للحل :
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
- الكسر الذي يمثل الجزء غير المظلل في الشكل التالي :
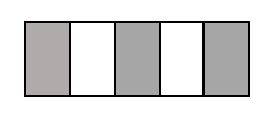
( أ) \( \frac{ ٣ }{ ٥ } \) ، ( ب) \( \frac{ ٢ }{ ٥ } \) ، ( ج) \( \frac{ ٢ }{ ٣ } \) ، ( د) \( \frac{ ٥ }{ ٣ } \)
شرح الإجابة : أولاً احسب جميع أجزاء الشكل وهي ٥ فتكتب في المقام ثم أحسب الأجزاء غير المظللة وعددها ٢ فتكتب في البسط .
فتكون الإجابة هي :
( ب) \( \frac{ ٢ }{ ٥ } \)
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
- حجم المُجسم المجاور :
( أ) ٢١ وحدة مكعبة ، ( ب) ١١ وحدة مكعبة ، ( ج) ١٥ وحدة مكعبة
شرح الإجابة : أعُد المكعبات في الجهة المسطحة من الشكل جهة اليسار وعددها ٥ مكعبات.
ثم الصفوف من اليسار إلى اليمين وعددها ٣ صفوف
فيكون حجم الشكل ٥ × ٣ = ١٥ وحدة مكعبة فالاختيار هو ( ج )
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
س ٢ / قارن مستعملاً ) < ، > ، = ( في كل مما يأتي :
٤٩٢٣ جم ( ) ٥ كجم ، \( \frac{ ٥ }{ ٧ } \) ( ) \( \frac{ ٢ }{ ٣ } \)
شرح الإجابة : للمقارنة بين الكيلو جرام والجرام يجب أن أُحول ٥ كجم إلى جرام بالضرب في ١٠٠٠ هكذا : ٥ × ١٠٠٠ = ٥٠٠٠ جم
إذن ٤٩٢٣ جم ( < ) ٥٠٠٠ جم
و للمقارنة بين \( \frac{ ٥ }{ ٧ } \) ( ) \( \frac{ ٢ }{ ٣ } \) يجب أن نوحد المقامات يعني يجب أن تكون المقامات متشابهة.
و أسهل طريقة لتوحيد المقامات هي طريقة المقص فأضرب الكسر \( \frac{ ٥ }{ ٧ } \) في ٣ و أضرب الكسر \( \frac{ ٢ }{ ٣ } \) في العدد ٧ ويكون شكل الكسرين بعد عملية الضرب هو : \( \frac{ ١٥ }{ ٢١ } \) ( ) \( \frac{ ١٤ }{ ٢١ } \) الآن أقارن بين الكسرين بالنظر إلى البسط .
وهذا شرح عملي :
فتكون الإجابة النهائية : \( \frac{ ١٥ }{ ٢١ } \) ( > ) \( \frac{ ١٤ }{ ٢١ } \)
إذن : \( \frac{ ٥ }{ ٧ } \) ( > ) \( \frac{ ٢ }{ ٣ } \)
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
س ٣ / قام أحمد ببناء سور لمنزلة على شكل مستطيل طوله ٥٥ متر وعرضه ٤٠ متر فاحسب محيطه ؟
الإجابة : بما أن الشكل هو مستطيل فأحسب المحيط بضرب ( ٢ × الطول ) + ( ٢ × العرض ) :
مح = ( ٢ط) + (٢ع )
= ( ٢ × ٥٥ ) + ( ٢ × ٤٠ )
= ١١٠ + ٨٠
= ١٩٠ م
أو أجمع أطوال الأضلاع :
المحيط = ٥٥ + ٤٠ + ٥٥ + ٤٠
= ١٩٠ م
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
س ٤ / أوجد الكسر المكافئ للكسر \( \frac{ ٤ }{ ٩ } \) ؟
شرح الإجابة : لإيجاد كسر مكافئ نضرب البسط والمقام في أي عدد من ٢ إلى ٩ والأسهل هو الضرب في العدد ٢ .
٢ × ٤ = ٨ ، ٢ × ٩ = ١٨
فالكسر المكافئ هو \( \frac{ ٨ }{ ١٨ } \)
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
س ٥ / رتب الكسور التالية من الأكبر إلى الأصغر :
\( \frac{ ٣ }{ ٧ } \) ، \( \frac{ ١ }{ ٢ } \) ، \( \frac{ ٥ }{ ١٤ } \)
شرح الإجابة : يجب توحيد المقامات لأستطيع ترتيب الكسور من الأكبر إلى الأصغر فالعدد ١٤ في جدول ضرب ٢ و ٧ فأضرب العدد ٢ في الكسر :
\( \frac{ ٣ }{ ٧ } \) فيكون الناتج : \( \frac{ ٦ }{ ١٤ } \)
وأضرب العدد ٧ في الكسر \( \frac{ ١ }{ ٢ } \) فيكون الناتج \( \frac{ ٧ }{ ١٤ } \) و هذا شكل الكسور قبل ترتيبها من الأكبر إلى الأصغر : \( \frac{ ٦ }{ ١٤ } \) ، \( \frac{ ٧ }{ ١٤ } \) ، \( \frac{ ٥ }{ ١٤ } \)
الآن أرتبها بحيث يكون الأكبر في اليمين ثم الأقل والأقل هكذا :
\( \frac{ ٧ }{ ١٤ } \) ، \( \frac{ ٦ }{ ١٤ } \) ، \( \frac{ ٥ }{ ١٤ } \)
وهذا شرح عملي لترتيب الكسور الاعتيادية :
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
س ٦ / يستعمل خالد ألواحا من الخشب مربعة الشكل طول كل منها ٣٠ سم . فاحسب مساحة اللوح ؟
الإجابة : بما أن الشكل مربع فأضرب طول الضلع × طول الضلع
م = ل × ل
= ٣٠ × ٣٠
= ٩٠٠ سنتيمتر مربع.
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ